
組裝公差分析
公差分析主要是探討一個描述工件組合後,其公差變動模式,一個好的公差分析模式可以預測組件公差能吻合實際組件公差界限有多少,其預測之機率愈大愈好。組裝公差分析可分成三種模式:最壞狀況模式(Worst-case model)、統計模式(Statistical model)和蒙地卡羅模式(Monte Carlo model).
概念
Dimension chain (sometimes called tolerance chain) is a closed loop of interrelated
dimensions. It consists of increasing, decreasing links and a single concluding link. In figures
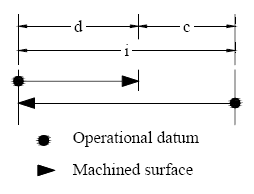
2-4 and 2-5, link i is the increasing link, d is a decreasing link and c is the concluding link.
Apparently, the concluding link c is the one whose tolerance is of interest and which is
produced indirectly. Increasing and decreasing links (both called contributing links) are the
ones that by increasing them, concluding link increases and decreases; respectively.
 |
 |
|---|---|
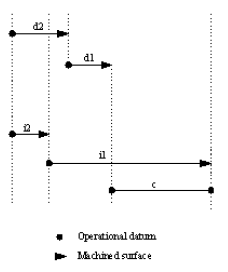
| Figure 1. Dimension Chain of c, 2 links, 1D | Figure 2.: Dimension Chain of c, 4 links, 1D |
The equation for evaluating the concluding link dimension is [Lin and Zhang (2001)]:
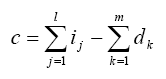 |
---------(1) |
|---|
Where:
Σi: The summation of the increasing link dimensions.
Σd: The summation of the decreasing link dimensions.
j: increasing links index.
k: decreasing links index.
l: number of increasing links.
m: number of decreasing links.
For figure 1 ,c can be found as:
c = i - d ------(2)
As for chain in figure 2, c can be found as:
c = (i1 + i2)-( d1 + d2) ------(3)
1. 最壞狀況模式(Worst-case model)
最壞狀況模式又稱上下偏差模式、極限模式、完全互換模式,此模式是以工件的最大及最小狀況組合,可以滿足完全互換性、組件公差最大.
In worst-case method, the concluding dimension’s tolerance Δc can be found as following:
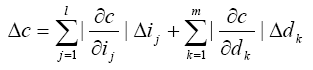 |
------(4) |
|---|
Referring to figure 2 and equations (3 and 4), the deviation of the concluding link is:
Δc = Δi1 + Δi2 + Δd1 + Δd2------(5)
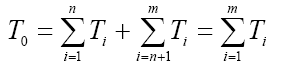
T0: 總公差
m: 零件之數目
Ti: 各零件之公差
2. 統計模式(Statistical model)
大量生產的產品,其零組件因為生產過程的變異所造成的公差呈統計分布,統計公差分析雖然可以估算結果尺寸公差的特性,但實際的分布情形還是無法掌握,統計模擬即是透過隨機取樣的原理
統計模式又稱均方根和模式(Root sum squared model),假設各零件公差都依據本身的特徵或加工條件會符合常態之鐘型曲線分佈,且分佈中心與公差帶中心值相同,分佈範圍與公差範圍也相同,組合公差為
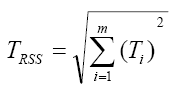 |
--------(6) |
|---|
m: 零件個數 , Ti :各零件之尺寸公差
另一種堆疊統計公差觀念如下
In statistical method, the concluding dimension’s tolerance Δc can be found as following:
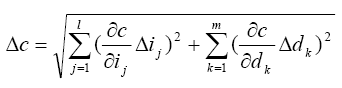 |
-----------(7) |
|---|
Referring to figure 2 and equations (5 and 7), the deviation of the concluding link is:
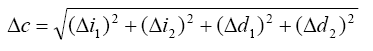 |
--------(8) |
|---|
Reduction of eliminated (貢獻度)
1. Statistical Contribution
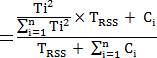 |
------------(9) |
|---|
2. Worst Case Contribution
| -------------------------(10) |
|---|
其中 Ci : Worst Case Clearance
蒙地卡羅模式(Monte Carlo model)
「蒙地卡羅方法」是一種數值方法,利用亂數取樣(Random sampling) 模擬來解決數學問題。在數學上,產生亂數,就是從一給
定的數集合中選出的數,若從集合中不按順序隨機選取其中數字,稱為亂數,如果選到的機率相同,視為均勻亂數,凡是所有具有隨機效應的過程,均可能以蒙地卡羅方法來大量模擬單一事件,藉統 計上平均值獲得某設定條件下實際最可能測量值。
蒙地卡羅方法的基本原理是將所有可能結果發生的機率,定義出一機率密度函數。將此機率密度函數累加成累積機率函數,調整其值最大值為1,此稱為正規化(Normalization)。這將正確反應出所有事件出現的總機率為1的機率特性,這也為亂數取樣與實際問題模擬建立起連結,也就是說將電腦所產生均勻分布於 [0, 1] 之間的亂數。本研究探討的公差問題,就是一種隨機問題,因為製造過程中變異所呈現的是隨機形式因此蒙地卡羅可以應用在公差分析的範疇.其方法是利用亂數產生器(Random number generator)在公差範圍內產生公差值,利用此公差值進行組裝,得到組合後的間隙.
處理蒙地卡羅模擬時,通常需要符合某種特定分布的亂數資料,因此就需要能夠符合特定分布的亂數產生器,其中又以常態分布最常 見,這是因為利用蒙地卡羅模擬的方法來分析的對象,通常都是呈現常態分布,在本研究中所要作的公差分析中,公差的產生在穩定的製程下應會呈常態分佈,但實際的加工情況下,上或下的偏公差需用不同的數學式 BETA 函數表示分佈曲線
| -------(11) |
|---|
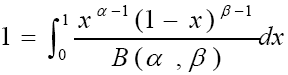
| 可寫成機率密度函數(P.d.f): f(x;α,β)= | 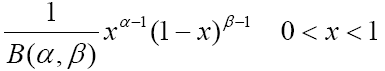 |
-------(12) |
|---|
其中以 α,β兩參數影響曲線分佈重要因素 , 當 α>β時 , 分佈向左傾,α=β時,常態分布;α<β時,分布向右偏,所以依據零件分布的情況而修改兩係數,在下面會運用圖表作詳細說明。
因此蒙地卡羅模式運用 Beta 函數有三個可調參數 , α,β,以及模擬次數,模擬次數可對照成生產數量,α及β代表尺寸是如何分佈
的重要參數,利用三個參數的搭配,來近似實際量產時的狀況。
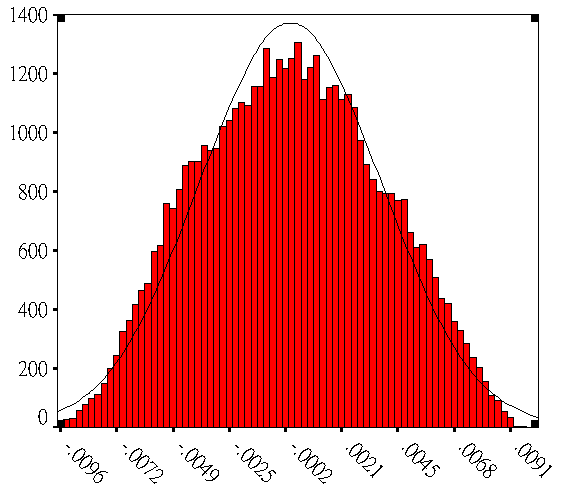
首先來探討對於Beta函數的α與β參數的給定與調整,在模擬分析時最常使用的是常態分佈來模擬公差情形,因此如何使用Beta函數來趨近常態分佈就變成很重要的事情,本段落給定幾種不同的α、β參數,並利用SPSS統計軟體的功能畫出直方圖來觀察結果,在此設定模擬次數為 50K .
(a) |
|
|---|---|
(c) |
|
(e) |
|
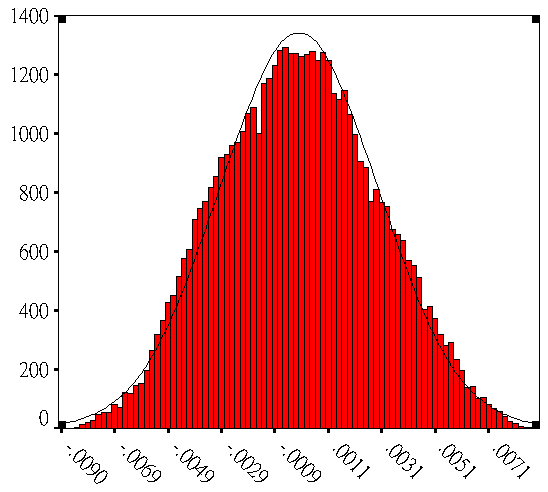
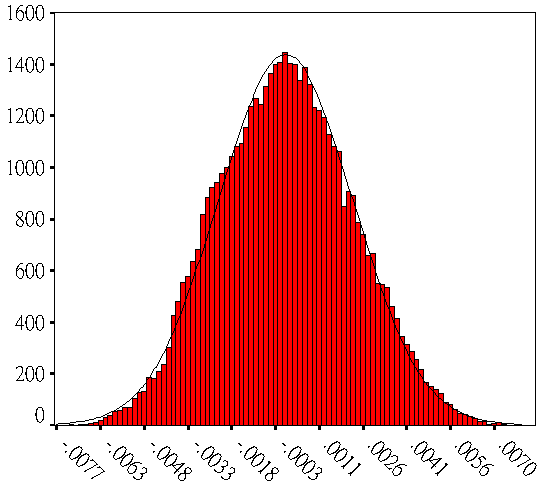
圖3 調整Beta函數中α與β參數逼近常態分佈與MatLab常態分佈圖的比較,(a)α=β=3,(b)α=β=5,(c)α=β=7,(d)α=β=9 , (e)MatLab 之常態分佈.
當α=β=5或7或9時,可觀察出分佈狀況都很逼近MatLab所顯示的常態分佈圖,因此在實際模擬時常用α=β=5的Beta函數來當作常態分佈的情形。上一段所提到因加工的不確定因素,將會造成公差呈現偏上限或是偏下限的情形發生,在此可利用Beta函數的特性,將公差分佈的趨勢偏上限或是偏下限,當α>β時Beta函數分佈的趨勢會偏上限,並且當α:β的比例越大時,Beta函數分佈偏上限的趨勢會越明顯,如圖3(a)和圖3(b)所示;相反的,當α<β時 Beta函數分佈的趨勢會偏下限,比例越大趨勢越明顯,如圖3(c)和圖3(d)所示;
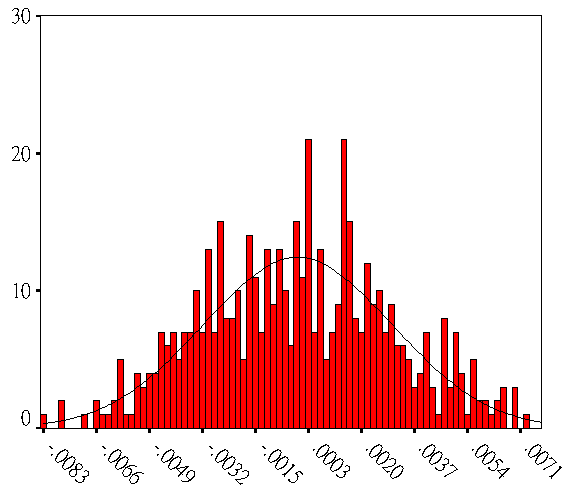
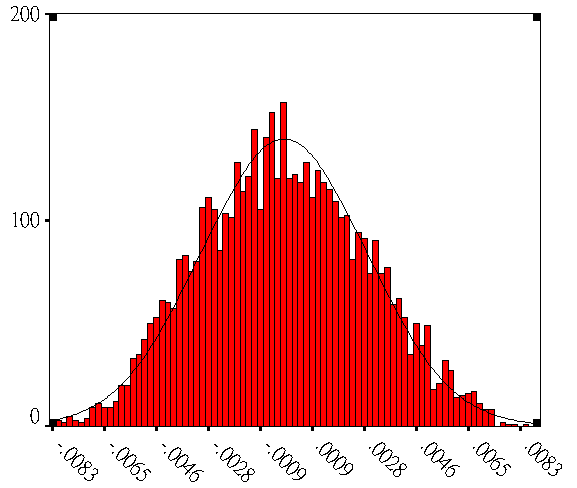
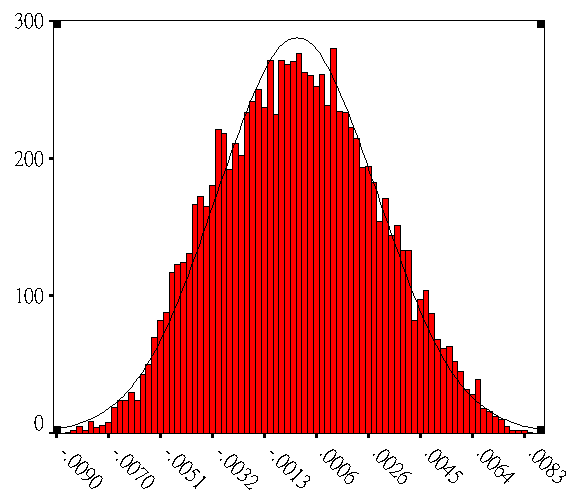
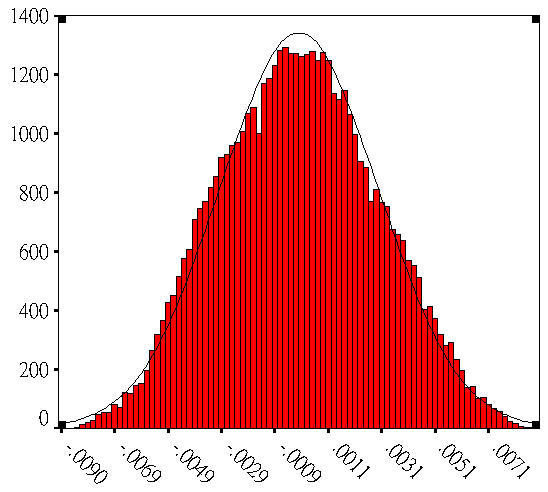
再來探討改變模擬次數影響分佈的情形,首先令α=β=5,再改變其模擬次數為500次、5000次、10000次以及50000次,並利用SPSS統計軟體的功能畫出直方圖來觀察結果,如圖2-7可發現,當模擬次數為10000次以下時如圖2-7(a)和圖2-7(b),發現Beta函數分佈會有失真的情形發生,將無法逼近常態分佈,但在模擬次數為10K 以上時 , 如圖2-7(a)和圖2-7(b)發現已相當接近常態分佈,故由此可知依實際需求 10 k 以上模擬次數較佳.
(a)
|
(b) |
|---|---|
(c)
|
|
圖3 . 蒙地卡羅模擬(a) 500 次數 (b) 1000 次數 (c) 10 k 次數 (d) 50 k 次數
實際例子演練
使用 Pro/Engineer 4.0 繪出 3D Parts , 後用 CETOL 做公差分析
備註:標準尺寸如以不對稱的公差標示,CETOL 會以對稱公差方式調整標準尺寸值計算出 Norminal .
案例 1.
條件:
1. part1 : 150±0.1
2. part2: 130 ±0.1
3. part3: 280 ±0.15

Reference :
Verify
Solved Nominal : Gap= 280-131-150=-1 (干涉)
TRSS=(0.1^2+0.1^2+0.15^2)^0.5=0.206
Standard Deviation (s) = TRSS /4.5 = 0.0458
Worst Case Range :
T0=0.1+0.1+0.15=0.35
Max=-1-0.35=-1.35
Min=-1+0.35=-0.65
Statisctical Range
min =-1+3 s = -1+3*(0.0458)=-0.8626
max =-1-3s=-1-3*(0.0458)=-1.1374
Sensitivity and Statistical Contribution Details
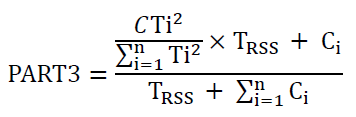
=(((0.15^2)*0.206/(0.1^2+0.1^2+0.15^2))+0)/(0.206+0)=0.5294=52.94%
part1,part2
=(((0.1^2)*0.206/(0.1^2+0.1^2+0.15^2))+0)/(0.206+0)=0.2353=23.53%
Worst Case Contribution Details
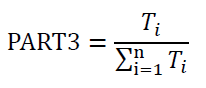
=0.15/0.35=0.4286=42.86%
Part1,2
=0.1/0.35=0.2857=28.57%
Conclusion
Because part1+part2 is interfered part3 , if base on worst case that max is -1.35 , min is -0.65 . if use statictcal mode then max is -1.1374 , min is -0.8626
案例 2.
以上題修改 part2 尺寸,分析會造成干涉的機率為多少.
條件:
1. part1 : 150±0.1
2. part2: 129.9 ±0.1
3. part3: 280 ±0.15
Pro/E 之 CETOL 分析出的結果如下:
Verify
Solved Nominal : Gap= 280-129.9-150=0.1 (間隙 )
TRSS=(0.1^2+0.1^2+0.15^2)^0.5=0.206
Standard Deviation (s) = TRSS /4.5 = 0.0458
Worst Case Range :
T0=0.1+0.1+0.15=0.35
Max=0.1+0.35=0.45
Min=0.1-0.35=-0.25
考慮間隙要大於0 , 如設計公差不變 .
則 normial = 0.1+0.25 = 0.35
Statistical Range
min =0.1-3 s = 0.1 - 3*(0.0458)=-0.0374
max =0.1+3s=0.1 + 3*(0.0458)=0.2374
Sensitivity and Statistical Contribution Details
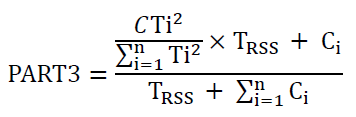
=(((0.15^2)*0.206/(0.1^2+0.1^2+0.15^2))+0)/(0.206+0)=0.5294=52.94%
part1,part2
=(((0.1^2)*0.206/(0.1^2+0.1^2+0.15^2))+0)/(0.206+0)=0.2353=23.53%
Worst Case Contribution Details
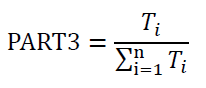
=0.15/0.35=0.4286=42.86%
Part1,2
=0.1/0.35=0.2857=28.57%
考慮會干涉的間隙是小於 0 , 機率計算如下
Z= (0 - 0.1) / 0.0458=-2.183
面積= 0.01454=1.454%
所以會組裝後干涉到 part 3 的機率為 1.454 %
如以不干涉的前提考慮則
查常態曲線面積表 Z最小為 -3.59
-3.59 = (0 - norminal) / 0.0458123
norminal = 0.1645
Conclusion
從此題可看出一些重點
1. 如以 worst case 考量雖然可看出最大干涉量為 0.25 但如要間隙大於 0 , 則需要將公差做小,增加零件的製作成本.
2. 以統計的計算方式 , 最大干涉量為 0.0374 , 機率只有 1.454 % .
3.如考量不能有干涉情形下, Worst Case 之 中間值增加為 0.35 , Statictical mode 之 中間值增加為 0.1645 , 由此可知以統計觀點考量,避免干涉的尺寸增加量較小 .
案例3.
手持裝置大部分都有放置 mic 如是接觸式因有上下殼與 pcb 件的製造公差,如 mic 與 pcb 預壓量不足,會有產生接觸性的問題.
Contents : Example3
網站資料:
|
|---|
 b)
b)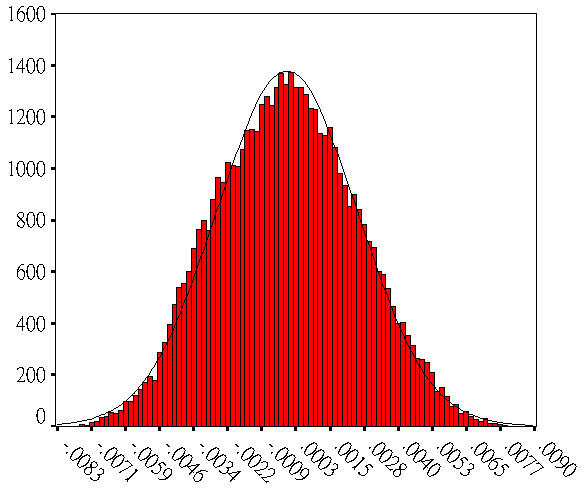
 d)
d)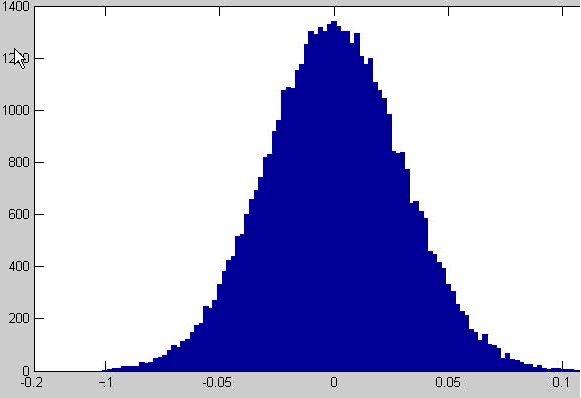
 (d)
(d)