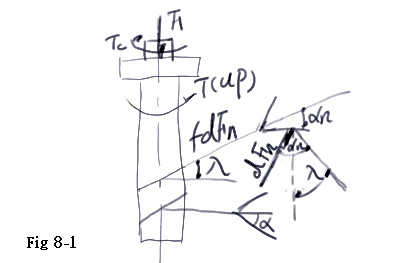
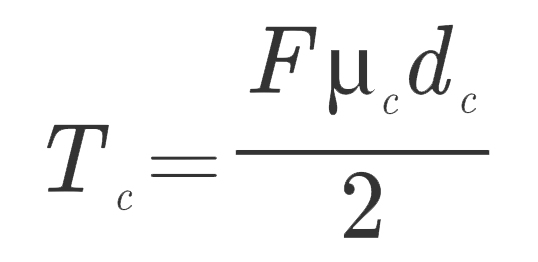The Design of Screws, Fasteners, and Connections

螺旋角(Helix angle)-螺旋線與通過軸線之面所夾之角.

導程角(Lead angle)-螺旋線與垂直軸線之面所夾之角.

導程(Lead)-沿螺旋線轉一圈,軸向前進之距離.

tanλ=l/(π*d_m) λ:導程角 l:導程 d_m:節圓直徑

統一標準螺紋:d_m=d-0.6495*p , d_r=d-1.226869*p.

梯形或方形螺紋: d_m=d-0.5p , d_r=d-p.

At:張應力面積(tensile - stress area)

At=(π/4)*((d_m+d_r)/2)²,σ=F/A_t

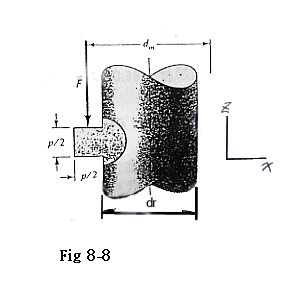
T_c:負重接觸力矩.

U_c:負重接觸摩擦係數.

d_c:負重接觸中數直徑.

傳動螺旋力學

ΣFy=0

-∫fdF_nsinλ-F+∫COSαnCOSλdF_n=0

∫dF_n=F/(COSαnCOSλ-f*sinλ)

ΣM_y=0

T-T_C-(d_m/2)*∫fcosλdFn-(d_m/2)*∫cosαn*sinλdFn=0

∴T=(d_m/2)*(sinλ*cosαn+fcosλ)*∫dFn+T_C

T=(F*d_m/2)*((sinλ*cosαn+fcosλ)/(COSλ*COSαn-f*sinλ))+T_C---(上升)<1>

T=(F*d_m/2)*((-sinλ*cosαn+fcosλ)/(COSλ*COSαn+f*sinλ))+T_C---(下降)<2>

螺旋壓力角與螺牙角轉換

tanαn=cosλ*tanα

As  <1>式右除以cosλcosαn

T=(F*d_m/2)*((tanλ+f*secαn)/(1-f*tanλ*secαn))+T_C---(上升)<3>

∵tanλ=l/(π*d_m)

∴

T=(F*d_m/2)*((l+f*π*d_m*secαn)/(π*dm-f*l*secαn))+T_C---(上升)<4>

As 方牙  α= α_n=0°, Secα_n=1

∴T=(F*d_m/2)*((l+f*π*d_m)/(π*dm-f*l))+T_C---(上升)<5>

   T=(F*d_m/2)*((-l+f*π*d_m)/(π*dm+f*l))+T_C---(下降)<6>

Self-locking(自鎖)

-l+f*π*d_m>0   ->  f>l/(pi*d_m)=tanλ    (f=tanΦ(摩擦角)).

mechanical efficiency

e=輸出功/輸入能=(F*l)/(T*2π)=((F*l)/(2π))/T=T₀/T

As f=f_c=0   (5) 式 變成 T₀=(F*l)/(2π).

螺栓本體應力

τ=(T*r)/J=16*T/(π*d_r³) , σ=F/A=(4*F)/(π*d_r²)

螺牙應力

Loading stress    σ_B=0.38F/(π*d_m*nt*(p/2))

bending stress

 σ_b=(M*C)/I

M=F*(1/2)*(P/2)=(F*P)/4

C/I=6/(b*h²)=6/(π*d_r*n_t*(P/2)²)=24/(π*d_r*n_t*P²)

∴σ_b=(6*F)/(π*d_r*n_t*P)

由Fig 8-8圖中得知

σ_x=(6*F)/(π*d_r*n_t*P)    σ_y=0

σ_z=(4*F)/(π*d_r²)     τ_xy=16*T/(π*d_r³)     

τ_yz=τ_zx=0

實驗證實,咬合的第一個螺牙承受38%的負載,第二個螺牙承受25%的負載,第三個承受18%的負載,而第七個螺牙則沒有承受負載,在使用前述的公式估算螺牙應力時,以0.38F取代F,而另n_t=1,將得到螺牙-螺帽組合中最大應力水準.