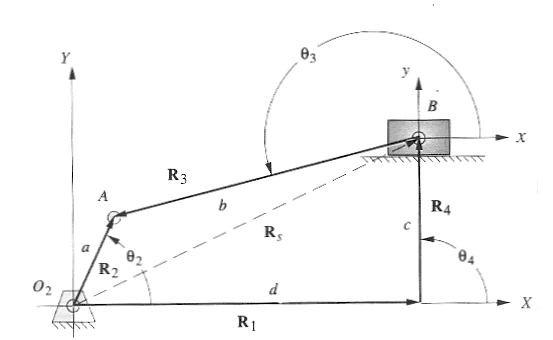
圖1.滑塊曲柄四連桿組的位置向量迴路

偏位是指滑塊的滑動軸線並不通過曲柄的固定軸線.

向量R₁和R₄為原點出發的向量R_S的正交分量.

連桿組的位置向量迴路方程式如下

R₂-R₃-R₄-R₁=0--------------------(1)

其方向角θ₃,一定要在向量的起始點量起.令各向量之長度分別為a,b,c,d ,將複數符號帶入位置向量迴路方程式．

ae^jθ2-be^jθ3-ce^jθ4-de^jθ1=0----------(2)

帶入尤拉等式

a(cosθ₂+jsinθ₂)-b(cosθ₃+jsinθ₃)-c(cosθ₄+jsinθ₄)-d(cosθ₁+jsinθ₁)=0------(3)

分解為實部與虛部

實部(x分量)

acosθ₂-bcosθ₃-ccosθ₄-dcosθ₁=0

∵θ₁=0

∴ acosθ₂-bcosθ₃-ccosθ₄-d=0 ----(3)

虛部(y分量)

jasinθ₂-jbsinθ₃-jcsinθ₄-jdsinθ₁=0

∵θ₁=0

∴ jasinθ₂-jbsinθ₃-jcsinθ₄=0 ------(4)

θ₂虛為獨立變數,連桿長度a,b及偏位量及角度θ₄均為已知.

θ₁=0,θ₄=90°

由(4)得

θ₃=sin^-1((asinθ₂-c)/b)----------------(5)           

d=acosθ₂-bcosθ₃----------------------(6)

因為向量座標方向設定的原則下,建議先釐清實際狀況,再重新推導向量關係式　而予以計算.